12. Nice guys finish first.

The Selfish Gene / 自私的基因
1Nice guys finish last. The phrase seems to have originated in the world of baseball, although some authorities claim priority for an alternative connotation. The American biologist Garrett Hardin used it to summarize the message of what may be called 'Sociobiology' or 'selfish genery'. It is easy to see its aptness. If we translate the colloquial meaning of 'nice guy' into its Darwinian equivalent, a nice guy is an individual that assists other members of its species, at its own expense, to pass their genes on to the next generation. Nice guys, then, seem bound to decrease in numbers: niceness dies a Darwinian death. But there is another, technical, interpretation of the colloquial word 'nice'. If we adopt this definition, which is not too far from the colloquial meaning, nice guys can finish first. This more optimistic conclusion is what this chapter is about.
2Remember the Grudgers of Chapter 10. These were birds that helped each other in an apparently altruistic way, but refused to help-bore a grudge against-individuals that had previously refused to help them.
3Grudgers came to dominate the population because they passed on more genes to future generations than either Suckers (who helped others indiscriminately, and were exploited) or Cheats (who tried ruthlessly to exploit everybody and ended up doing each other down). The story of the Grudgers illustrated an important general principle, which Robert Trivers called 'reciprocal altruism'. As we saw in the example of the cleaner fish, reciprocal altruism is not confined to members of a single species. It is at work in all relationships that are called symbiotic-for instance the ants milking their aphid 'cattle'. Since Chapter 10 was written, the American political scientist Robert Axelrod (working partly in collaboration with W.
4D. Hamilton, whose name has cropped up on so many pages of this book), has taken the idea of reciprocal altruism on in exciting new directions. It was Axelrod who coined the technical meaning of the word
5'nice' to which I alluded in my opening paragraph.
6Axelrod, like many political scientists, economists, mathematicians and psychologists, was fascinated by a simple gambling game called Prisoner's Dilemma. It is so simple that I have known clever men misunderstand it completely, thinking that there must be more to it! But its simplicity is deceptive.
7Whole shelves in libraries are devoted to the ramifications of this beguiling game. Many influential people think it holds the key to strategic defence planning, and that we should study it to prevent a third world war. As a biologist, I agree with Axelrod and Hamilton that many wild animals and plants are engaged in ceaseless games of Prisoner's Dilemma, played out in evolutionary time.
8In its original, human, version, here is how the game is played. There is a 'banker', who adjudicates and pays out winnings to the two players.
9Suppose that I am playing against you (though, as we shall see, 'against' is precisely what we don't have to be). There are only two cards in each of our hands, labelled cooperate and defect. To play, we each choose one of our cards and lay it face down on the table.
10Face down so that neither of us can be influenced by the other's move: in effect, we move simultaneously. We now wait in suspense for the banker to turn the cards over. The suspense is because our winnings depend not just on which card we have played (which we each know), but on the other player's card too (which we don't know until the banker reveals it).
11Since there are 2 x 2 cards, there are four possible outcomes. For each outcome, our winnings are as follows (quoted in dollars in deference to the North American origins of the game): Outcome I: We have both played cooperate. The banker pays each of us $300. This respectable sum is called the Reward for mutual cooperation.
12Outcome 11: We have both played defect. The banker fines each of us $10. This is called the Punishment for mutual defection.
13Outcome III: You have played cooperate; I have played defect. The banker pays me $500 (the Temptation to defect) and fines you (the Sucker) $100.
14Outcome IV: You have played defect; I have played cooperate. The banker pays you the Temptation payoff of $500 and fines me, the Sucker, $100.
15Outcomes III and IV are obviously mirror images: one player does very well and the other does very badly. In outcomes I and 11 we do as well as one another, but I is better for both of us than II. The exact quantities of money don't matter. It doesn't even matter how many of them are positive (payments) and how many of them, if any, are negative (fines).
16What matters, for the game to qualify as a true Prisoner's Dilemma, is their rank order. The Temptation to defect must be better than the Reward for mutual cooperation, which must be better than the Punishment for mutual defection, which must be better than the Sucker's payoff. (Strictly speaking, there is one further condition for the game to qualify as a true Prisoner's Dilemma: the average of the Temptation and the Sucker payoffs must not exceed the Reward. The reason for this additional condition will emerge later.) The four outcomes are summarized in the payoff matrix in Figure A.

17Figure A. Payoffs to me from various outcomes of the Prisoner's Dilemma game Now,
18why the 'dilemma'? To see this, look at the payoff matrix and imagine the thoughts that might go through my head as I play against you. I know that there are only two cards you can play, cooperate and defect. Let's consider them in order. If you have played defect (this means we have to look at the right hand column), the best card I could have played would have been defect too. Admittedly I'd have suffered the penalty for mutual defection, but if I'd cooperated I'd have got the Sucker's payoff which is even worse. Now let's turn to the other thing you could have done (look at the left hand column), play the cooperate card.
19Once again defect is the best thing I could have done. If I had cooperated we'd both have got the rather high score of $300. But if I'd defected I'd have got even more-$500. The conclusion is that, regardless of which card you play, my best move is Always Defect.
20So I have worked out by impeccable logic that, regardless of what you do, I must defect. And you, with no less impeccable logic, will work out just the same thing. So when two rational players meet, they will both defect, and both will end up with a fine or a low payoff. Yet each knows perfectly well that, if only they had both played cooperate, both would have obtained the relatively high reward for mutual cooperation ($300 in our example). That is why the game is called a dilemma, why it seems so maddeningly paradoxical, and why it has even been proposed that there ought to be a law against it.
21'Prisoner' comes from one particular imaginary example. The currency in this case is not money but prison sentences. Two men- call them Peterson and Moriarty-are in jail, suspected of collaborating in a crime.
22Each prisoner, in his separate cell, is invited to betray his colleague (defect) by turning King's Evidence against him. What happens depends upon what both prisoners do, and neither knows what the other has done. If Peterson throws the blame entirely on Moriarty, and Moriarty renders the story plausible by remaining silent (cooperating with his erstwhile and, as it turns out, treacherous friend), Moriarty gets a heavy jail sentence while Peterson gets off scot-free, having yielded to the Temptation to defect. If each betrays the other, both are convicted of the crime, but receive some credit for giving evidence and get a somewhat reduced, though still stiff, sentence, the Punishment for mutual defection.
23If both cooperate (with each other, not with the authorities) by refusing to speak, there is not enough evidence to convict either of them of the main crime, and they receive a small sentence for a lesser offence, the Reward for mutual cooperation. Although it may seem odd to call a jail sentence a 'reward', that is how the men would see it if the alternative was a longer spell behind bars. You will notice that, although the 'payoffs' are not in dollars but in jail sentences, the essential features of the game are preserved (look at the rank order of desirability of the four outcomes). If you put yourself in each prisoner's place, assuming both to be motivated by rational self-interest and remembering that they cannot talk to one another to make a pact, you will see that neither has any choice but to betray the other, thereby condemning both to heavy sentences.
24Is there any way out of the dilemma? Both players know that, whatever their opponent does, they themselves cannot do better than defect; yet both also know that, if only both had cooperated, each one would have done better. If only . .. if only . .. if only there could be some way of reaching agreement, some way of reassuring each player that the other can be trusted not to go for the selfish jackpot, some way of policing the agreement.
25In the simple game of Prisoner's Dilemma, there is no way of ensuring trust. Unless at least one of the players is a really saintly sucker, too good for this world, the game is doomed to end in mutual defection with its paradoxically poor result for both players. But there is another version of the game.
26It is called the 'Iterated' or 'Repeated' Prisoner's Dilemma. The iterated game is more complicated, and in its complication lies hope.
27The iterated game is simply the ordinary game repeated an indefinite number of times with the same players. Once again you and I face each other, with a banker sitting between. Once again we each have a hand of just two cards, labelled cooperate and defect. Once again we move by each playing one or other of these cards and the banker shells out, or levies fines, according to the rules given above. But now, instead of that being the end of the game, we pick up our cards and prepare for another round. The successive rounds of the game give us the opportunity to build up trust or mistrust, to reciprocate or placate, forgive or avenge. In an indefinitely long game, the important point is that we can both win at the expense of the banker, rather than at the expense of one another.
28After ten rounds of the game, I could theoretically have won as much as $5,000, but only if you have been extraordinarily silly (or saintly) and played cooperate every time, in spite of the fact that I was consistently defecting. More realistically, it is easy for each of us to pick up $3,000 of the banker's money by both playing cooperate on all ten rounds of the game. For this we don't have to be particularly saintly, because we can both see, from the other's past moves, that the other is to be trusted. We can, in effect, police each other's behaviour. Another thing that is quite likely to happen is that neither of us trusts the other: we both play defect for all ten rounds of the game, and the banker gains $100 in fines from each of us. Most likely of all is that we partially trust one another, and each play some mixed sequence of cooperate and defect, ending up with some intermediate sum of money.
29The birds in Chapter 10 who removed ticks from each other's feathers were playing an iterated Prisoner's Dilemma game. How is this so? It is important, you remember, for a bird to pull off his own ticks, but he cannot reach the top of his own head and needs a companion to do that for him. It would seem only fair that he should return the favour later.
30But this service costs a bird time and energy, albeit not much. If a bird can get away with cheating- with having his own ticks removed but then refusing to reciprocate-he gains all the benefits without paying the costs.
31Rank the outcomes, and you'll find that indeed we have a true game of Prisoner's Dilemma. Both cooperating (pulling each other's ticks off) is pretty good, but there is still a temptation to do even better by refusing to pay the costs of reciprocating. Both defecting (refusing to pull ticks off) is pretty bad, but not so bad as putting effort into pulling another's ticks off and still ending up infested with ticks oneself. The payoff matrix is Figure B.
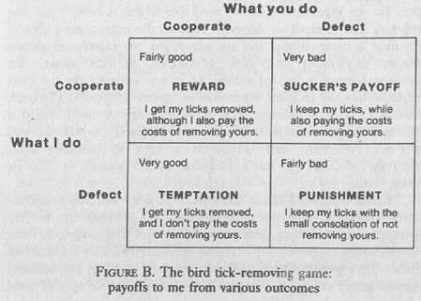
32Figure B. The bird tick-removing game: payoffs to me from various outcomes
33But this is only one example. The more you think about it, the more you realize that life is riddled with Iterated Prisoner's Dilemma games, not just human life but animal and plant life too. Plant life?
34Yes, why not?
35Remember that we are not talking about conscious strategies (though at times we might be), but about strategies in the 'Maynard Smithian' sense, strategies of the kind that genes might preprogram. Later we shall meet plants, various animals and even bacteria, all playing the game of Iterated Prisoner's Dilemma. Meanwhile, let's explore more fully what is so important about iteration.
36Unlike the simple game, which is rather predictable in that defect is the only rational strategy, the iterated version offers plenty of strategic scope.
37In the simple game there are only two possible strategies, cooperate and defect. Iteration, however, allows lots of conceivable strategies, and it is by no means obvious which one is best. The following, for instance, is just one among thousands: 'cooperate most of the time, but on a random 10 per cent of rounds throw in a defect'. Or strategies might be conditional upon the past history of the game. My 'Grudger' is an example of this; it has a good memory for faces, and although fundamentally cooperative it defects if the other player has ever defected before. Other strategies might be more forgiving and have shorter memories.
38Clearly the strategies available in the iterated game are limited only by our ingenuity. Can we work out which is best? This was the task that Axelrod set himself. He had the entertaining idea of running a competition, and he advertised for experts in games theory to submit strategies. Strategies, in this sense, are preprogrammed rules for action, so it was appropriate for contestants to send in their entries in computer language. Fourteen strategies were submitted. For good measure Axelrod added a fifteenth, called Random, which simply played cooperate and defect randomly, and served as a kind of baseline 'non-strategy': if a strategy can't do better than Random, it must be pretty bad.
39Axelrod translated all 15 strategies into one common programming language, and set them against one another in one big computer. Each strategy was paired off in turn with every other one (including a copy of itself) to play Iterated Prisoner's Dilemma. Since there were 15 strategies, there were 15 x 15, or 225 separate games going on in the computer.
40When each pairing had gone through 200 moves of the game, the winnings were totalled up and the winner declared.
41We are not concerned with which strategy won against any particular opponent. What matters is which strategy accumulated the most 'money', summed over all its 15 pairings. 'Money' means simply 'points', awarded according to the following scheme: mutual Cooperation, 3 points; Temptation to defect, 5 points; Punishment for mutual defection, 1 point (equivalent to a light fine in our earlier game); Sucker's payoff, 0 points (equivalent to a heavy fine in our earlier game).
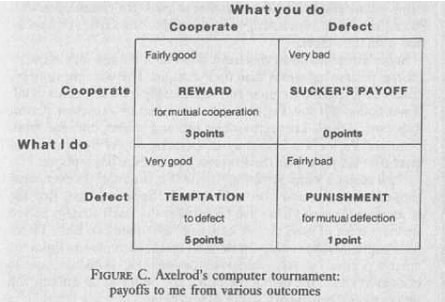
42Figure C. Axelrod's computer tournament: payoffs to me from various outcomes
43The maximum possible score that any strategy could achieve was 15,000 (200 rounds at 5 points per round, for each of 15 opponents). The minimum possible score was 0.
44Needless to say, neither of these two extremes was realized. The most that a strategy can realistically hope to win in an average one of its 15 pairings cannot be much more than 600 points. This is what two players would each receive if they both consistently cooperated, scoring 3 points for each of the 200 rounds of the game. If one of them succumbed to the temptation to defect, it would very probably end up with fewer points than 600 because of retaliation by the other player (most of the submitted strategies had some kind of retaliatory behaviour built into them). We can use 600 as a kind of benchmark for a game, and express all scores as a percentage of this benchmark. On this scale it is theoretically possible to score up to 166 per cent (1000 points), but in practice no strategy's average score exceeded 600.
45Remember that the 'players' in the tournament were not humans but computer programs, preprogrammed strategies. Their human authors played the same role as genes programming bodies (think of Chapter 4's computer chess and the Andromeda computer). You can think of the strategies as miniature 'proxies' for their authors. Indeed, one author could have submitted more than one strategy {although it would have been cheating-and Axelrod would presumably not have allowed it-for an author to 'pack' the competition with strategies, one of which received the benefits of sacrificial cooperation from the others).
46Some ingenious strategies were submitted, though they were, of course, far less ingenious than their authors. The winning strategy, remarkably, was the simplest and superficially least ingenious of all. It was called Tit for Tat, and was submitted by Professor Anatol Rapoport, a well-known psychologist and games theorist from Toronto. Tit for Tat begins by cooperating on the first move and thereafter simply copies the previous move of the other player.
47How might a game involving Tit for Tat proceed? As ever, what happens depends upon the other player. Suppose, first, that the other player is also Tit for Tat (remember that each strategy played against copies of itself as well as against the other 14). Both Tit for Tats begin by cooperating. In the next move, each player copies the other's previous move, which was cooperate. Both continue to cooperate until the end of the game, and both end up with the full 100 per cent 'benchmark' score of 600 points.
48Now suppose Tit for Tat plays against a strategy called Naive Prober.
49Naive Prober wasn't actually entered in Axelrod's competition, but it is instructive nevertheless. It is basically identical to Tit for Tat except that, once in a while, say on a random one in ten moves, it throws in a gratuitous defection and claims the high Temptation score. Until Naive Prober tries one of its probing defections the players might as well be two Tit for Tats. A long and mutually profitable sequence of cooperation seems set to run its course, with a comfortable 100 per cent benchmark score for both players. But suddenly, without warning, say on the eighth move, Naive Prober defects. Tit for Tat, of course, has played cooperate on this move, and so is landed with the Sucker's payoff of 0 points.
50Naive Prober appears to have done well, since it has obtained 5 points from that move. But in the next move Tit for Tat 'retaliates'. It plays defect, simply following its rule of imitating the opponent's previous move.
51Naive Prober meanwhile, blindly following its own built-in copying rule, has copied its opponent's cooperate move. So it now collects the Sucker's payoff of 0 points, while Tit for Tat gets the high score of 5. In the next move, Naive Prober-rather unjustly one might think-'retaliates' against Tit for Tat's defection. And so the alternation continues. During these alternating runs both players receive on average 2.5 points per move (the average of 5 and 0). This is lower than the steady 3 points per move that both players can amass in a run of mutual cooperation. So, when Naive Prober plays against Tit for Tat, both do worse than when Tit for Tat plays against another Tit for Tat. And when Naive Prober plays against another Naive Prober, both tend to do, if anything, even worse still, since runs of reverberating defection tend to get started earlier.
52Now consider another strategy, called Remorseful Prober. Remorseful Prober is like Naive Prober, except that it takes active steps to break out of runs of alternating recrimination. To do this it needs a slightly longer
53'memory' than either Tit for Tat or Naive Prober. Remorseful Prober remembers whether it has just spontaneously defected, and whether the result was prompt retaliation. If so, it 'remorsefully' allows its opponent
54'one free hit' without retaliating. This means that runs of mutual recrimination are nipped in the bud. If you now work through an imaginary game between Remorseful Prober and Tit for Tat, you'll find that runs of would-be mutual retaliation are promptly scotched. Most of the game is spent in mutual cooperation, with both players enjoying the consequent generous score. Remorseful Prober does better against Tit for Tat than Naive Prober does, though not as well as Tit for Tat does against itself.
55Some of the strategies entered in Axelrod's tournament were much more sophisticated than either Remorseful Prober or Naive Prober, but they too ended up with fewer points, on average, than simple Tit for Tat. Indeed the least successful of all the strategies (except Random) was the most elaborate. It was submitted by 'Name withheld'-a spur to pleasing speculation: Some eminence grise in the Pentagon? The head of the CIA?
56Henry Kissinger? Axelrod himself? I suppose we shall never know.
57It isn't all that interesting to examine the details of the particular strategies that were submitted. This isn't a book about the ingenuity of computer programmers. It is more interesting to classify strategies according to certain categories, and examine the success of these broader divisions. The most important category that Axelrod recognizes is 'nice'. A nice strategy is defined as one that is never the first to defect Tit for Tat is an example. It is capable of defecting, but it does so only in retaliation. Both Naive Prober and Remorseful Prober are nasty strategies because they sometimes defect, however rarely, when not provoked. Of the 15 strategies entered in the tournament, 8 were nice. Significantly, the 8 top-scoring strategies were the very same 8 nice strategies, the 7
58nasties trailing well behind. Tit for Tat obtained an average of 5045 points: 84 per cent of our benchmark of 600, and a good score. The other nice strategies scored only slightly less, with scores ranging from 83.4 per cent down to 786 per cent. There is a big gap between this score and the 66.8 per cent obtained by Graaskamp, the most successful of all the nasty strategies. It seems pretty convincing that nice guys do well in this game.
59Another of Axelrod's technical terms is 'forgiving'. A forgiving strategy is one that, although it may retaliate, has a short memory. It is swift to overlook old misdeeds. Tit for Tat is a forgiving strategy.
60It raps a defector over the knuckles instantly but, after that, lets bygones be bygones.
61Chapter 10's Grudger is totally unforgiving. Its memory lasts the entire game. It never forgets a grudge against a player who has ever defected against it, even once. A strategy formally identical to Grudger was entered in Axelrod's tournament under the name of Friedman, and it didn't do particularly well.
62Of all the nice strategies (note that it is technically nice, although it is totally unforgiving), Grudger/Friedman did next to worst. The reason unforgiving strategies don't do very well is that they can't break out of runs of mutual recrimination, even when their opponent is 'remorseful'.
63It is possible to be even more forgiving than Tit for Tat. Tit for Two Tats allows its opponents two defections in a row before it eventually retaliates.
64This might seem excessively saintly and magnanimous. Nevertheless Axelrod worked out that, if only somebody had submitted Tit for Two Tats, it would have won the tournament. This is because it is so good at avoiding runs of mutual recrimination.
65So, we have identified two characteristics of winning strategies: niceness and forgivingness. This almost utopian-sounding conclusion-that niceness and forgivingness pay-came as a surprise to many of the experts, who had tried to be too cunning by submitting subtly nasty strategies; while even those who had submitted nice strategies had not dared anything so forgiving as Tit for Two Tats.
66Axelrod announced a second tournament. He received 62 entries and again added Random, making 63 in all. This time, the exact number of moves per game was not fixed at 200 but was left open, for a good reason that I shall come to later. We can still express scores as a percentage of the 'benchmark', or 'always cooperate' score, even though that benchmark needs more complicated calculation and is no longer a fixed 600 points.
67Programmers in the second tournament had all been provided with the results of the first, including Axelrod's analysis of why Tit for Tat and other nice and forgiving strategies had done so well. It was only to be expected that the contestants would take note of this background information, in one way or another. In fact, they split into two schools of thought. Some reasoned that niceness and forgivingness were evidently winning qualities, and they accordingly submitted nice, forgiving strategies. John Maynard Smith went so far as to submit the super-forgiving Tit for Two Tats. The other school of thought reasoned that lots of their colleagues, having read Axelrod's analysis, would now submit nice, forgiving strategies. They therefore submitted nasty strategies, trying to exploit these anticipated softies!
68But once again nastiness didn't pay. Once again, Tit for Tat, submitted by Anatol Rapoport, was the winner, and it scored a massive 96 per cent of the benchmark score. And again nice strategies, in general, did better than nasty ones. All but one of the top 15 strategies were nice, and all but one of the bottom 15 were nasty. But although the saintly Tit for Two Tats would have won the first tournament if it had been submitted, it did not win the second. This was because the field now included more subtle nasty strategies capable of preying ruthlessly upon such an out-and-out softy.
69This underlines an important point about these tournaments. Success for a strategy depends upon which other strategies happen to be submitted. This is the only way to account for the difference between the second tournament, in which Tit for Two Tats was ranked well down the list, and the first tournament, which Tit for Two Tats would have won.
70But, as I said before, this is not a book about the ingenuity of computer programmers. Is there an objective way in which we can judge which is the truly best strategy, in a more general and less arbitrary sense?
71Readers of earlier chapters will already be prepared to find the answer in the theory of evolutionarily stable strategies.
72I was one of those to whom Axelrod circulated his early results, with an invitation to submit a strategy for the second tournament. I didn't do so, but I did make another suggestion. Axelrod had already begun to think in ESS terms, but I felt that this tendency was so important that I wrote to him suggesting that he should get in touch with W. D. Hamilton, who was then, though Axelrod didn't know it, in a different department of the same university, the University of Michigan. He did indeed immediately contact Hamilton, and the result of their subsequent collaboration was a brilliant joint paper published in the journal Science in 1981, a paper that won the Newcomb Cleveland Prize of the American Association for the Advancement of Science. In addition to discussing some delightfully way-out biological examples of iterated prisoner's dilemmas, Axelrod and Hamilton gave what I regard as due recognition to the ESS approach.
73Contrast the ESS approach with the 'round-robin' system that Axelrod's two tournaments followed. A round-robin is like a football league. Each strategy was matched against each other strategy an equal number of times. The final score of a strategy was the sum of the points it gained against all the other strategies. To be successful in a round-robin tournament, therefore, a strategy has to be a good competitor against all the other strategies that people happen to have submitted. Axelrod's name for a strategy that is good against a wide variety of other strategies is 'robust'. Tit for Tat turned out to be a robust strategy. But the set of strategies that people happen to have submitted is an arbitrary set. This was the point that worried us above. It just so happened that in Axelrod's original tournament about half the entries were nice. Tit for Tat won in this climate, and Tit for Two Tats would have won in this climate if it had been submitted. But suppose that nearly all the entries had just happened to be nasty. This could very easily have occurred. After all, 6 out of the 14 strategies submitted were nasty. If 13 of them had been nasty, Tit for Tat wouldn't have won. The 'climate' would have been wrong for it. Not only the money won, but the rank order of success among strategies, depends upon which strategies happen to have been submitted; depends, in other words, upon something as arbitrary as human whim. How can we reduce this arbitrariness? By 'thinking ESS'.
74The important characteristic of an evolutionarily stable strategy, you will remember from earlier chapters, is that it carries on doing well when it is already numerous in the population of strategies.
75To say that Tit for Tat, say, is an ESS, would be to say that Tit for Tat does well in a climate dominated by Tit for Tat. This could be seen as a special kind of 'robustness'. As evolutionists we are tempted to see it as the only kind of robustness that matters. Why does it matter so much? Because, in the world of Darwinism, winnings are not paid out as money; they are paid out as offspring. To a Darwinian, a successful strategy is one that has become numerous in the population of strategies. For a strategy to remain successful, it must do well specifically when it is numerous, that is in a climate dominated by copies of itself.
76Axelrod did, as a matter of fact, run a third round of his tournament as natural selection might have run it, looking for an ESS. Actually he didn't call it a third round, since he didn't solicit new entries but used the same 63 as for Round 2. I find it convenient to treat it as Round 3, because I think it differs from the two 'round-robin' tournaments more fundamentally than the two round-robin tournaments differ from each other.
77Axelrod took the 63 strategies and threw them again into the computer to make 'generation 1' of an evolutionary succession. In 'generation 1', therefore, the 'climate' consisted of an equal representation of all 63
78strategies. At the end of generation 1, winnings to each strategy were paid out, not as 'money' or 'points', but as offsprings identical to their (asexual) parents. As generations went by, some strategies became scarcer and eventually went extinct. Other strategies became more numerous. As the proportions changed, so, consequently, did the 'climate' in which future moves of the game took place.
79Eventually, after about 1000 generations, there were no further changes in proportions, no further changes in climate. Stability was reached.
80Before this, the fortunes of the various strategies rose and fell, just as in my computer simulation of the Cheats, Suckers, and Grudgers. Some of the strategies started going extinct from the start, and most were extinct by generation 200. Of the nasty strategies, one or two of them began by increasing in frequency, but their prosperity, like that of Cheat in my simulation, was short-lived. The only nasty strategy to survive beyond generation 200 was one called Harrington. Harrington's fortunes rose steeply for about the first 150 generations. Thereafter it declined rather gradually, approaching extinction around generation 1,000. Harrington did well temporarily for the same reason as my original Cheat did. It exploited softies like Tit for Two Tats (too forgiving) while these were still around. Then, as the softies were driven extinct, Harrington followed them, having no easy prey left.
81The field was free for 'nice' but
82'provocable' strategies like Tit for Tat.
83Tit for Tat itself, indeed, came out top in five out of six runs of Round 3, just as it had in Rounds 1 and 2. Five other nice but provocable strategies ended up nearly as successful (frequent in the population) as Tit for Tat; indeed, one of them won the sixth run. When all the nasties had been driven extinct, there was no way in which any of the nice strategies could be distinguished from Tit for Tat or from each other, because they all, being nice, simply played cooperate against each other.
84A consequence of this indistinguishability is that, although Tit for Tat seems like an ESS, it is strictly not a true ESS. To be an ESS, remember, a strategy must not be invadable, when it is common, by a rare, mutant strategy. Now it is true that Tit for Tat cannot be invaded by any nasty strategy, but another nice strategy is a different matter. As we have just seen, in a population of nice strategies they will all look and behave exactly like one another: they will all cooperate all the time. So any other nice strategy, like the totally saintly Always Cooperate, although admittedly it will not enjoy a positive selective advantage over Tit for Tat, can nevertheless drift into the population without being noticed. So technically Tit for Tat is not an ESS.
85You might think that since the world stays just as nice, we could as well regard Tit for Tat as an ESS.
86But alas, look what happens next. Unlike Tit for Tat, Always Cooperate is not stable against invasion by nasty strategies such as Always Defect. Always Defect does well against Always Cooperate, since it gets the high 'Temptation' score every time. Nasty strategies like Always Defect will come in to keep down the numbers of too nice strategies like Always Cooperate.
87But although Tit for Tat is strictly speaking not a true ESS, it is probably fair to treat some sort of mixture of basically nice but retaliatory 'Tit for Tat-like' strategies as roughly equivalent to an ESS in practice. Such a mixture might include a small admixture of nastiness. Robert Boyd and Jeffrey Lorberbaum, in one of the more interesting follow-ups to Axelrod's work, looked at a mixture of Tit for Two Tats and a strategy called Suspicious Tit for Tat. Suspicious Tit for Tat is technically nasty, but it is not very nasty. It behaves just like Tit for Tat itself after the first move, but-this is what makes it technically nasty-it does defect on the very first move of the game. In a climate entirely dominated by Tit for Tat, Suspicious Tit for Tat does not prosper, because its initial defection triggers an unbroken run of mutual recrimination. When it meets a Tit for Two Tats player, on the other hand, Tit for Two Tats's greater forgivingness nips this recrimination in the bud. Both players end the game with at least the 'benchmark', all C, score and with Suspicious Tit for Tat scoring a bonus for its initial defection. Boyd and Lorberbaum showed that a population of Tit for Tat could be invaded, evolutionarily speaking, by a mixture of Tit for Two Tats and Suspicious Tit for Tat, the two prospering in each other's company. This combination is almost certainly not the only combination that could invade in this kind of way.
88There are probably lots of mixtures of slightly nasty strategies with nice and very forgiving strategies that are together capable of invading. Some might see this as a mirror for familiar aspects of human life.
89Axelrod recognized that Tit for Tat is not strictly an ESS, and he therefore coined the phrase 'collectively stable strategy' to describe it. As in the case of true ESSs, it is possible for more than one strategy to be collectively stable at the same time. And again, it is a matter of luck which one comes to dominate a population. Always Defect is also stable, as well as Tit for Tat. In a population that has already come to be dominated by Always Defect, no other strategy does better. We can treat the system as bistable, with Always Defect being one of the stable points, Tit for Tat (or some mixture of mostly nice, retaliatory strategies) the other stable point. Whichever stable point comes to dominate the population first will tend to stay dominant.
90But what does 'dominate' mean, in quantitative terms? How many Tit for Tats must there be in order for Tit for Tat to do better than Always Defect?
91That depends upon the detailed payoffs that the banker has agreed to shell out in this particular game.
92All we can say in general is that there is a critical frequency, a knife-edge. On one side of the knife- edge the critical frequency of Tit for Tat is exceeded, and selection will favour more and more Tit for Tats. On the other side of the knife-edge the critical frequency of Always Defect is exceeded, and selection will favour more and more Always Defects. We met the equivalent of this knife-edge, you will remember, in the story of the Grudgers and Cheats in Chapter 10.
93It obviously matters, therefore, on which side of the knife-edge a population happens to start. And we need to know how it might happen that a population could occasionally cross from one side of the knife-edge to the other. Suppose we start with a population already sitting on the Always Defect side.
94The few Tit for Tat individuals don't meet each other often enough to be of mutual benefit. So natural selection pushes the population even further towards the Always Defect extreme. If only the population could just manage, by random drift, to get itself over the knife-edge, it could coast down the slope to the Tit for Tat side, and everyone would do much better at the banker's (or 'nature's') expense.
95But of course populations have no group will, no group intention or purpose. They cannot strive to leap the knife-edge. They will cross it only if the undirected forces of nature happen to lead them across.
96How could this happen? One way to express the answer is that it might happen by 'chance'. But 'chance' is just a word expressing ignorance. It means 'determined by some as yet unknown, or unspecified, means'. We can do a little better than 'chance'. We can try to think of practical ways in which a minority of Tit for Tat individuals might happen to increase to the critical mass. This amounts to a quest for possible ways in which Tit for Tat individuals might happen to cluster together in sufficient numbers that they can all benefit at the banker's expense.
97This line of thought seems to be promising, but it is rather vague. How exactly might mutually resembling individuals find themselves clustered together, in local aggregations? In nature, the obvious way is through genetic relatedness-kinship. Animals of most species are likely to find themselves living close to their sisters, brothers and cousins, rather than to random members of the population. This is not necessarily through choice. It follows automatically from 'viscosity' in the population.
98Viscosity means any tendency for individuals to continue living close to the place where they were born. For instance, through most of history, and in most parts of the world (though not, as it happens, in our modern world), individual humans have seldom strayed more than a few miles from their birthplace. As a result, local clusters of genetic relatives tend to build up. I remember visiting a remote island off the west coast of Ireland, and being struck by the fact that almost everyone on the island had the most enormous jug-handle ears. This could hardly have been because large ears suited the climate (there are strong offshore winds). It was because most of the inhabitants of the island were close kin of one another.
99Genetic relatives will tend to be alike not just in facial features but in all sorts of other respects as well. For instance, they will tend to resemble each other with respect to genetic tendencies to play-or not to play-Tit for Tat. So even if Tit for Tat is rare in the population as a whole, it may still be locally common. In a local area, Tit for Tat individuals may meet each other often enough to prosper from mutual cooperation, even though calculations that take into account only the global frequency in the total population might suggest that they are below the 'knife-edge' critical frequency.
100If this happens, Tit for Tat individuals, cooperating with one another in cosy little local enclaves, may prosper so well that they grow from small local clusters into larger local clusters. These local clusters may grow so large that they spread out into other areas, areas that had hitherto been dominated, numerically, by individuals playing Always Defect. In thinking of these local enclaves, my Irish island is a misleading parallel because it is physically cut off. Think, instead, of a large population in which there is not much movement, so that individuals tend to resemble their immediate neighbours more than their more distant neighbours, even though there is continuous interbreeding all over the whole area.
101Coming back to our knife-edge, then, Tit for Tat could surmount it. All that is required is a little local clustering, of a sort that will naturally tend to arise in natural populations. Tit for Tat has a built-in gift, even when rare, for crossing the knife-edge over to its own side. It is as though there were a secret passage underneath the knife-edge. But that secret passage contains a one-way valve: there is an asymmetry. Unlike Tit for Tat, Always Defect, though a true ESS, cannot use local clustering to cross the knife-edge. On the contrary. Local clusters of Always Defect individuals, far from prospering by each other's presence, do especially badly in each other's presence. Far from quietly helping one another at the expense of the banker, they do one another down. Always Defect, then, unlike Tit for Tat, gets no help from kinship or viscosity in the population.
102So, although Tit for Tat may be only dubiously an ESS, it has a sort of higher-order stability. What can this mean? Surely, stable is stable. Well, here we are taking a longer view. Always Defect resists invasion for a long time. But if we wait long enough, perhaps thousands of years, Tit for Tat will eventually muster the numbers required to tip it over the knife-edge, and the population will flip. But the reverse will not happen. Always Defect, as we have seen, cannot benefit from clustering, and so does not enjoy this higher-order stability.
103Tit for Tat, as we have seen, is 'nice', meaning never the first to defect, and 'forgiving', meaning that it has a short memory for past misdeeds. I now introduce another of Axelrod's evocative technical terms. Tit for Tat is also 'not envious'. To be envious, in Axelrod's terminology, means to strive for more money than the other player, rather than for an absolutely large quantity of the banker's money.
104To be non-envious means to be quite happy if the other player wins just as much money as you do, so long as you both thereby win more from the banker. Tit for Tat never actually 'wins' a game. Think about it and you'll see that it cannot score more than its 'opponent' in any particular game because it never defects except in retaliation. The most it can do is draw with its opponent.
105But it tends to achieve each draw with a high, shared score. Where Tit for Tat and other nice strategies are concerned, the very word 'opponent' is inappropriate. Sadly, however, when psychologists set up games of Iterated Prisoner's Dilemma between real humans, nearly all players succumb to envy and therefore do relatively poorly in terms of money. It seems that many people, perhaps without even thinking about it, would rather do down the other player than cooperate with the other player to do down the banker. Axelrod's work has shown what a mistake this is.
106It is only a mistake in certain kinds of game. Games theorists divide games into 'zero sum' and 'nonzero sum'. A zero sum game is one in which a win for one player is a loss for the other. Chess is zero sum, because the aim of each player is to win, and this means to make the other player lose.
107Prisoner's Dilemma, however, is a nonzero sum game.
108There is a banker paying out money, and it is possible for the two players to link arms and laugh all the way to the bank.
109This talk of laughing all the way to the bank reminds me of a delightful line from Shakespeare: The first thing we do, let's kill all the lawyers.
1102 Henry VI
111In what are called civil 'disputes' there is often in fact great scope for cooperation. What looks like a zero sum confrontation can, with a little goodwill, be transformed into a mutually beneficial nonzero sum game.
112Consider divorce. A good marriage is obviously a nonzero sum game, brimming with mutual cooperation. But even when it breaks down there are all sorts of reasons why a couple could benefit by continuing to cooperate, and treating their divorce, too, as nonzero sum. As if child welfare were not a sufficient reason, the fees of two lawyers will make a nasty dent in the family finances. So obviously a sensible and civilized couple begin by going together to see one lawyer, don't they?
113Well, actually no. At least in England and, until recently, in all fifty states of the USA, the law, or more strictly-and significantly-the lawyers' own professional code, doesn't allow them to. Lawyers must accept only one member of a couple as a client. The other person is turned from the door, and either has no legal advice at all or is forced to go to another lawyer.
114And that is when the fun begins. In separate chambers but with one voice, the two lawyers immediately start referring to 'us' and 'them'. 'Us', you understand, doesn't mean me and my wife; it means me and my lawyer against her and her lawyer. When the case comes to court, it is actually listed as 'Smith versus Smith'! It is assumed to be adversarial, whether the couple feel adversarial or not, whether or not they have specifically agreed that they want to be sensibly amicable. And who benefits from treating it as an 'I win, you lose' tussle? The chances are, only the lawyers.
115The hapless couple have been dragged into a zero sum game. For the lawyers, however, the case of Smith v. Smith is a nice fat nonzero sum game, with the Smiths providing the payoffs and the two professionals milking their clients' joint account in elaborately coded cooperation. One way in which they cooperate is to make proposals that they both know the other side will not accept. This prompts a counter proposal that, again, both know is unacceptable. And so it goes on. Every letter, every telephone call exchanged between the cooperating 'adversaries' adds another wad to the bill. With luck, this procedure can be dragged out for months or even years, with costs mounting in parallel. The lawyers don't get together to work all this out. On the contrary, it is ironically their scrupulous separateness that is the chief instrument of their cooperation at the expense of the clients. The lawyers may not even be aware of what they are doing. Like the vampire bats that we shall meet in a moment, they are playing to well-ritualized rules. The system works without any conscious overseeing or organizing. It is all geared to forcing us into zero sum games. Zero sum for the clients, but very much nonzero sum for the lawyers.
116What is to be done? The Shakespeare option is messy. It would be cleaner to get the law changed. But most parliamentarians are drawn from the legal profession, and have a zero sum mentality. It is hard to imagine a more adversarial atmosphere than the British House of Commons. (The law courts at least preserve the decencies of debate. As well they might, since 'my learned friend and I' are cooperating very nicely all the way to the bank.) Perhaps well-meaning legislators and, indeed, contrite lawyers should be taught a little game theory. It is only fair to add that some lawyers play exactly the opposite role, persuading clients who are itching for a zero sum fight that they would do better to reach a nonzero sum settlement out of court.
117What about other games in human life? Which are zero sum and which nonzero sum? And-because this is not the same thing- which aspects of life do we perceive as zero or nonzero sum? Which aspects of human life foster 'envy', and which foster cooperation against a 'banker'? Think, for instance, about wage-bargaining and 'differentials'. When we negotiate our pay-rises, are we motivated by 'envy', or do we cooperate to maximize our real income? Do we assume, in real life as well as in psychological experiments, that we are playing a zero sum game when we are not? I simply pose these difficult questions. To answer them would go beyond the scope of this book.
118Football is a zero sum game. At least, it usually is. Occasionally it can become a nonzero sum game.
119This happened in 1977 in the English Football League (Association Football or 'Soccer'; the other games called football-Rugby Football, Australian Football, American Football, Irish Football, etc., are also normally zero sum games). Teams in the Football League are split into four divisions. Clubs play against other clubs within their own division, accumulating points for each win or draw throughout the season. To be in the First Division is prestigious, and also lucrative for a club since it ensures large crowds. At the end of each season, the bottom three clubs in the First Division are relegated to the Second Division for the next season. Relegation seems to be regarded as a terrible fate, worth going to great efforts to avoid.
120May 18th 1977 was the last day of that year's football season. Two of the three relegations from the First Division had already been determined, but the third relegation was still in contention. It would definitely be one of three teams, Sunderland, Bristol, or Coventry. These three teams, then, had everything to play for on that Saturday. Sunderland were playing against a fourth team (whose tenure in the First Division was not in doubt). Bristol and Coventry happened to be playing against each other.
121It was known that, if Sunderland lost their game, then Bristol and Coventry needed only to draw against each other in order to stay in the First Division. But if Sunderland won, then the team relegated would be either Bristol or Coventry, depending on the outcome of their game against each other. The two crucial games were theoretically simultaneous. As a matter of fact, however, the Bristol-Coventry game happened to be running five minutes late. Because of this, the result of the Sunderland game became known before the end of the Bristol-Coventry game. Thereby hangs this whole complicated tale.
122For most of the game between Bristol and Coventry the play was, to quote one contemporary news report, 'fast and often furious', an exciting (if you like that sort of thing) ding-dong battle. Some brilliant goals from both sides had seen to it that the score was 2-all by the eightieth minute of the match. Then, two minutes before the end of the game, the news came through from the other ground that Sunderland had lost.
123Immediately, the Coventry team manager had the news flashed up on the giant electronic message board at the end of the ground. Apparently all 22 players could read, and they all realized that they needn't bother to play hard any more. A draw was all that either team needed in order to avoid relegation. Indeed, to put effort into scoring goals was now positively bad policy since, by taking players away from defence, it carried the risk of actually losing-and being relegated after all. Both sides became intent on securing a draw. To quote the same news report: 'Supporters who had been fierce rivals seconds before when Don Gillies fired in an 80th minute equaliser for Bristol, suddenly joined in a combined celebration. Referee Ron Challis watched helpless as the players pushed the ball around with little or no challenge to the man in possession.' What had previously been a zero sum game had suddenly, because of a piece of news from the outside world, become a nonzero sum game. In the terms of our earlier discussion, it is as if an external 'banker' had magically appeared, making it possible for both Bristol and Coventry to benefit from the same outcome, a draw.
124Spectator sports like football are normally zero sum games for a good reason. It is more exciting for crowds to watch players striving mightily against one another than to watch them conniving amicably.
125But real life, both human life and plant and animal life, is not set up for the benefit of spectators.
126Many situations in real life are, as a matter of fact, equivalent to nonzero sum games. Nature often plays the role of 'banker', and individuals can therefore benefit from one another's success. They do not have to do down rivals in order to benefit themselves. Without departing from the fundamental laws of the selfish gene, we can see how cooperation and mutual assistance can flourish even in a basically selfish world. We can see how, in Axelrod's meaning of the term, nice guys may finish first.
127But none of this works unless the game is iterated. The players must know (or 'know') that the present game is not the last one between them.
128In Axelrod's haunting phrase, the 'shadow of the future' must be long.
129But how long must it be? It can't be infinitely long. From a theoretical point of view it doesn't matter how long the game is; the important thing is that neither player should know when the game is going to end.
130Suppose you and I were playing against each other, and suppose we both knew that the number of rounds in the game was to be exactly 100. Now we both understand that the 100th round, being the last, will be equivalent to a simple one-off game of Prisoner's Dilemma. Therefore the only rational strategy for either of us to play on the 100th round will be defect, and we can each assume that the other player will work that out and be fully resolved to defect on the last round. The last round can therefore be written off as predictable. But now the 99th round will be the equivalent of a one-off game, and the only rational choice for each player on this last but one game is also defect. The 98th round succumbs to the same reasoning, and so on back. Two strictly rational players, each of whom assumes that the other is strictly rational, can do nothing but defect if they both know how many rounds the game is destined to run. For this reason, when games theorists talk about the Iterated or Repeated Prisoner's Dilemma game, they always assume that the end of the game is unpredictable, or known only to the banker.
131Even if the exact number of rounds in the game is not known for certain, in real life it is often possible to make a statistical guess as to how much longer the game is likely to last. This assessment may become an important part of strategy. If I notice the banker fidget and look at his watch, I may well conjecture that the game is about to be brought to an end, and I may therefore feel tempted to defect. If I suspect that you too have noticed the banker fidgeting, I may fear that you too may be contemplating defection. I will probably be anxious to get my defection in first. Especially since I may fear that you are fearing that I. . .
132The mathematician's simple distinction between the one-off Prisoner's Dilemma game and the Iterated Prisoner's Dilemma game is too simple.
133Each player can be expected to behave as if he possessed a continuously updated estimate of how long the game is likely to go on. The longer his estimate, the more he will play according to the mathematician's expectations for the true iterated game: in other words, the nicer, more forgiving, less envious he will be. The shorter his estimate of the future of the game, the more he will be inclined to play according to the mathematician's expectations for the one-off game: the nastier, and less forgiving will he be. Axelrod draws a moving illustration of the importance of the shadow of the future from a remarkable phenomenon that grew up during the First World War, the so-called live- and-let-live system. His source is the research of the historian and sociologist Tony Ashworth. It is quite well known that at Christmas British and German troops briefly fraternized and drank together in no-man's-land. Less well known, but in my opinion more interesting, is the fact that unofficial and unspoken nonaggression pacts, a 'live-and-let-live' system, flourished all up and down the front lines for at least two years starting in 1914. A senior British officer, on a visit to the trenches, is quoted as being astonished to observe German soldiers walking about within rifle range behind their own line.
134'Our men appeared to take no notice. I privately made up my mind to do away with that sort of thing when we took over; such things should not be allowed. These people evidently did not know there was a war on. Both sides apparently believed in the policy of "live-and-let-live". ' The theory of games and the Prisoner's Dilemma had not been invented in those days but, with hindsight, we can see pretty clearly what was going on, and Axelrod provides a fascinating analysis. In the entrenched warfare of those times, the shadow of the future for each platoon was long. That is to say, each dug-in group of British soldiers could expect to be facing the same dug-in group of Germans for many months. Moreover, the ordinary soldiers never knew when, if ever, they were going to be moved; army orders are notoriously arbitrary, capricious and incomprehensible to those receiving them. The shadow of the future was quite long enough, and indeterminate enough, to foster the development of a Tit for Tat type of cooperation. Provided, that is, that the situation was equivalent to a game of Prisoner's Dilemma.
135To qualify as a true Prisoner's Dilemma, remember, the payoffs have to follow a particular rank order. Both sides must see mutual cooperation (CC) as preferable to mutual defection. Defection while the other side cooperates (DC) is even better if you can get away with it. Cooperation while the other side defects (CD) is worst of all. Mutual defection (DD) is what the general staff would like to see. They want to see their own chaps, keen as mustard, potting Jerries (or Tommies) whenever the opportunity arises.
136Mutual cooperation was undesirable from the generals' point of view, because it wasn't helping them to win the war. But it was highly desirable from the point of view of the individual soldiers on both sides.
137They didn't want to be shot. Admittedly-and this takes care of the other payoff conditions needed to make the situation a true Prisoner's Dilemma-they probably agreed with the generals in preferring to win the war rather than lose it. But that is not the choice that faces an individual soldier. The outcome of the entire war is unlikely to be materially affected by what he, as an individual, does. Mutual cooperation with the particular enemy soldiers facing you across no-man's-land most definitely does affect your own fate, and is greatly preferable to mutual defection, even though you might, for patriotic or disciplinary reasons, marginally prefer to defect (DC) if you could get away with it It seems that the situation was a true prisoner's dilemma. Something like Tit for Tat could be expected to grow up, and it did.
138The locally stable strategy in any particular part of the trench lines was not necessarily Tit for Tat itself. Tit for Tat is one of a family of nice, retaliatory but forgiving strategies, all of which are, if not technically stable, at least difficult to invade once they arise. Three Tits for a Tat, for instance, grew up in one local area according to a contemporary account.
139We go out at night in front of the trenches... The German working parties are also out, so it is not considered etiquette to fire. The really nasty things are rifle grenades ... They can kill as many as eight or nine men if they do fall into a trench ... But we never use ours unless the Germans get particularly noisy, as on their system of retaliation three for every one of ours come back.
140It is important, for any member of the Tit for Tat family of strategies, that the players are punished for defection. The threat of retaliation must always be there. Displays of retaliatory capability were a notable feature of the live-and-let-live system. Crack shots on both sides would display their deadly virtuosity by firing, not at enemy soldiers, but at inanimate targets close to the enemy soldiers, a technique also used in Western films (like shooting out candle flames). It does not seem ever to have been satisfactorily answered why the two first operational atomic bombs were used-against the strongly voiced wishes of the leading physicists responsible for developing them-to destroy two cities instead of being deployed in the equivalent of spectacularly shooting out candles.
141An important feature of Tit for Tat-like strategies is that they are forgiving. This, as we have seen, helps to damp down what might otherwise become long and damaging runs of mutual recrimination.
142The importance of damping down retaliation is dramatized by the following memoir by a British (as if the first sentence left us in any doubt) officer: I was having tea with A company when we heard a lot of shouting and went to investigate. We found our men and the Germans standing on their respective parapets. Suddenly a salvo arrived but did no damage.
143Naturally both sides got down and our men started swearing at the Germans, when all at once a brave German got on to his parapet and shouted out 'We are very sorry about that; we hope no one was hurt.
144It is not our fault, it is that damned Prussian artillery.' Axelrod comments that this apology 'goes well beyond a merely instrumental effort to prevent retaliation. It reflects moral regret for having violated a situation of trust, and it shows concern that someone might have been hurt.' Certainly an admirable and very brave German.
145Axelrod also emphasizes the importance of predictability and ritual in maintaining a stable pattern of mutual trust. A pleasing example of this was the 'evening gun' fired by British artillery with clockwork regularity at a certain part of the line. In the words of a German soldier: At seven it came- so regularly that you could set your watch by it... It always had the same objective, its range was accurate, it never varied laterally or went beyond or fell short of the mark... There were even some inquisitive fellows who crawled out... a little before seven, in order to see it burst.
146The German artillery did just the same thing, as the following account from the British side shows: So regular were they [the Germans] in their choice of targets, times of shooting, and number of rounds fired, that... Colonel Jones ... knew to a minute where the next shell would fall. His calculations were very accurate, and he was able to take what seemed to uninitiated Staff Officers big risks, knowing that the shelling would stop before he reached the place being shelled.
147Axelrod remarks that such 'rituals of perfunctory and routine firing sent a double message. To the high command they conveyed aggression, but to the enemy they conveyed peace.' The live-and-let-live system could have been worked out by verbal negotiation, by conscious strategists bargaining round a table. In fact it was not. It grew up as a series of local conventions, through people responding to one another's behaviour; the individual soldiers were probably hardly aware that the growing up was going on. This need not surprise us. The strategies in Axelrod's computer were definitely unconscious. It was their behaviour that defined them as nice or nasty, as forgiving or unforgiving, envious or the reverse. The programmers who designed them may have been any of these things, but that is irrelevant.
148A nice, forgiving, non-envious strategy could easily be programmed into a computer by a very nasty man. And vice versa. A strategy's niceness is recognized by its behaviour, not by its motives (for it has none) nor by the personality of its author (who has faded into the background by the time the program is running in the computer). A computer program can behave in a strategic manner, without being aware of its strategy or, indeed, of anything at all.
149We are, of course, entirely familiar with the idea of unconscious strategists, or at least of strategists whose consciousness, if any, is irrelevant. Unconscious strategists abound in the pages of this book.
150Axelrod's programs are an exellent model for the way we, throughout the book, have been thinking of animals and plants, and indeed of genes. So it is natural to ask whether his optimistic conclusions- about the success of non-envious, forgiving niceness-also apply in the world of nature. The answer is yes, of course they do. The only conditions are that nature should sometimes set up games of Prisoner's Dilemma, that the shadow of the future should be long, and that the games should be nonzero sum games. These conditions are certainly met, all round the living kingdoms.
151Nobody would ever claim that a bacterium was a conscious strategist, yet bacterial parasites are probably engaged in ceaseless games of Prisoner's Dilemma with their hosts and there is no reason why we should not attribute Axelrodian adjectives-forgiving, non-envious, and so on-to their strategies. Axelrod and Hamilton point out that normally harmless or beneficial bacteria can turn nasty, even causing lethal sepsis, in a person who is injured. A doctor might say that the person's 'natural resistance'
152is lowered by the injury. But perhaps the real reason is to do with games of Prisoner's Dilemma. Do the bacteria, perhaps, have something to gain, but usually keep themselves in check? In the game between human and bacteria, the 'shadow of the future' is normally long since a typical human can be expected to live for years from any given starting-point. A seriously wounded human, on the other hand, may present a potentially much shorter shadow of the future to his bacterial guests. The 'Temptation to defect' correspondingly starts to look like a more attractive option than the 'Reward for mutual cooperation'. Needless to say, there is no suggestion that the bacteria work all this out in their nasty little heads! Selection on generations of bacteria has presumably built into them an unconscious rule of thumb which works by purely biochemical means.
153Plants, according to Axelrod and Hamilton, may even take revenge, again obviously unconsciously.
154Fig trees and fig wasps share an intimate cooperative relationship. The fig that you eat is not really a fruit. There is a tiny hole at the end, and if you go into this hole (you'd have to be as small as a fig wasp to do so, and they are minute: thankfully too small to notice when you eat a fig), you find hundreds of tiny flowers lining the walls. The fig is a dark indoor hothouse for flowers, an indoor pollination chamber. And the only agents that can do the pollinating are fig wasps.
155The tree, then, benefits from harbouring the wasps. But what is in it for the wasps? They lay their eggs in some of the tiny flowers, which the larvae then eat. They pollinate other flowers within the same fig.
156'Defecting', for a wasp, would mean laying eggs in too many of the flowers in a fig and pollinating too few of them. But how could a fig tree 'retaliate'?
157According to Axelrod and Hamilton, 'It turns out in many cases that if a fig wasp entering a young fig does not pollinate enough flowers for seeds and instead lays eggs in almost all, the tree cuts off the developing fig at an early stage. All progeny of the wasp then perish.' A bizarre example of what appears to be a Tit for Tat arrangement in nature was discovered by Eric Fischer in a hermaphrodite fish, the sea bass. Unlike us, these fish don't have their sex determined at conception by their chromosomes. Instead, every individual is capable of performing both female and male functions. In any one spawning episode they shed either eggs or sperm. They form monogamous pairs and, within the pair, take turns to play the male and female roles. Now, we may surmise that any individual fish, if it could get away with it, would 'prefer' to play the male role all the time, because the male role is cheaper. Putting it another way, an individual that succeeded in persuading its partner to play the female most of the time would gain all the benefits of 'her' economic investment in eggs, while 'he' has resources left over to spend on other things, for instance on mating with other fish.
158In fact, what Fischer observed was that the fishes operate a system of pretty strict alternation. This is just what we should expect if they are playing Tit for Tat. And it is plausible that they should, because it does appear that the game is a true Prisoner's Dilemma, albeit a somewhat complicated one. To play the cooperate card means to play the female role when it is your turn to do so. Attempting to play the male role when it is your turn to play the female is equivalent to playing the defect card.
159Defection is vulnerable to retaliation: the partner can refuse to play the female role next time it is 'her' (his?) turn to do so, or 'she' can simply terminate the whole relationship. Fischer did indeed observe that pairs with an uneven sharing of sex roles tended to break up.
160A question that sociologists and psychologists sometimes ask is why blood donors (in countries, such as Britain, where they are not paid) give blood. I find it hard to believe that the answer lies in reciprocity or disguised selfishness in any simple sense. It is not as though regular blood donors receive preferential treatment when they come to need a transfusion. They are not even issued with little gold stars to wear.
161Maybe I am naive, but I find myself tempted to see it as a genuine case of pure, disinterested altruism.
162Be that as it may, blood-sharing in vampire bats seems to fit the Axelrod model well. We learn this from the work of G.
163S. Wilkinson.
164Vampires, as is well known, feed on blood at night. It is not easy for them to get a meal, but if they do it is likely to be a big one. When dawn comes, some individuals will have been unlucky and return completely empty, while those individuals that have managed to find a victim are likely to have sucked a surplus of blood. On a subsequent night the luck may run the other way. So, it looks like a promising case for a bit of reciprocal altruism. Wilkinson found that those individuals who struck lucky on any one night did indeed sometimes donate blood, by regurgitation, to their less fortunate comrades. Out of 110 regurgitations that Wilkinson witnessed, 77 could easily be understood as cases of mothers feeding their children, and many other instances of blood-sharing involved other kinds of genetic relatives. There still remained, however, some examples of blood-sharing among unrelated bats, cases where the 'blood is thicker than water' explanation would not fit the facts. Significantly the individuals involved here tended to be frequent roostmates-they had every opportunity to interact with one another repeatedly, as is required for an Iterated Prisoner's Dilemma. But were the other requirements for a Prisoner's Dilemma met? The payoff matrix in Figure D is what we should expect if they were.
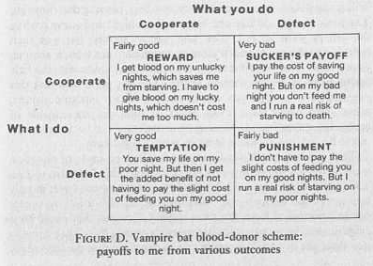
165Figure D. Vampire bat blood-donor scheme: payoffs to me from various outcomes.
166Do vampire economics really conform to this table? Wilkinson looked at the rate at which starved vampires lose weight. From this he calculated the time it would take a sated bat to starve to death, the time it would take an empty bat to starve to death, and all intermediates. This enabled him to cash out blood in the currency of hours of prolonged life. He found, not really surprisingly, that the exchange rate is different, depending upon how starved a bat is. A given amount of blood adds more hours to the life of a highly starved bat ' than to a less starved one. In other words, although the act of donating blood would increase the chances of the donor dying, this increase was small compared with the increase in the recipient's chances of surviving. Economically speaking, then, it seems plausible that vampire economics conform to the rules of a Prisoner's Dilemma. The blood that the donor gives up is less precious to her (social groups in vampires are female groups) than the same quantity of blood is to the recipient. On her unlucky nights she really would benefit enormously from a gift of blood.
167But on her lucky nights she would benefit slightly, if she could get away with it, from defecting- refusing to donate blood. 'Getting away with it', of course, means something only if the bats are adopting some kind of Tit for Tat strategy.
168So, are the other conditions for the evolution of Tit for Tat reciprocation met?
169In particular, can these bats recognize one another as individuals?
170Wilkinson did an experiment with captive bats, proving that they can.
171The basic idea was to take one bat away for a night and starve it while the others were all fed. The unfortunate starved bat was then returned to the roost, and Wilkinson watched to see who, if anyone, gave it food. The experiment was repeated many times, with the bats taking turns to be the starved victim. The key point was that this population of captive bats was a mixture of two separate groups, taken from caves many miles apart. If vampires are capable of recognizing their friends, the experimentally starved bat should turn out to be fed only by those from its own original cave.
172That is pretty much what happened. Thirteen cases of donation were observed. In twelve out of these thirteen, the donor bat was an 'old friend' of the starved victim, taken from the same cave; in only one out of the thirteen cases was the starved victim fed by a 'new friend', not taken from the same cave. Of course this could be a coincidence but we can calculate the odds against this. They come to less than one in 500. It is pretty safe to conclude that the bats really
173were biased in favour of feeding old friends rather than strangers from a different cave.
174Vampires are great mythmakers. To devotees of Victorian Gothic they are dark forces that terrorize by night, sapping vital fluids, sacrificing an innocent life merely to gratify a thirst. Combine this with that other Victorian myth, nature red in tooth and claw, and aren't vampires the very incarnation of deepest fears about the world of the selfish gene? As for me, I am sceptical of all myths. If we want to know where the truth lies in particular cases, we have to look. What the Darwinian corpus gives us is not detailed expectations about particular organisms. It gives us something subtler and more valuable: understanding of principle. But if we must have myths, the real facts about vampires could tell a different moral tale. To the bats themselves, not only is blood thicker than water. They rise above the bonds of kinship, forming their own lasting ties of loyal blood-brotherhood. Vampires could form the vanguard of a comfortable new myth, a myth of sharing, mutualistic cooperation. They could herald the benignant idea that, even with selfish genes at the helm, nice guys can finish first.
